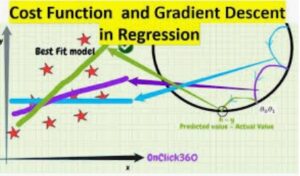
In continuation of previous post i.e. Gradient Descent and Cost function , we touched upon the below points. For instance..
- Forward propagation to calculate the Loss.
- Backward propagation to the know the derivation in order to get the new values of W and b for subsequent Gradient descent iterations.
However, Now its time to deep dive and see how things are derived for one GD iteration.
Case Study:
Firstly, Let’s assume we have a basic neural network which takes 2 features x1 and x2 as input and try to predict the value of Y.
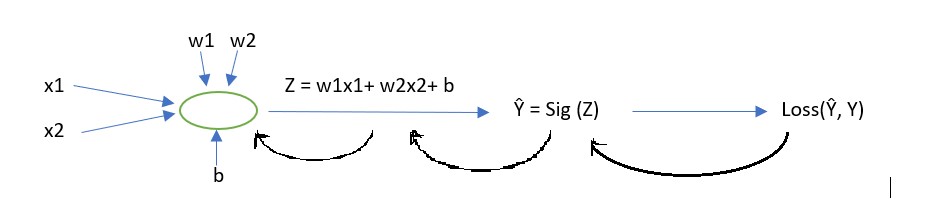
Backward propagation Steps:
In the first step of backward propagation we calculate the derivation of the loss function with respect to Ŷ in below way (Refer Fig 1.).
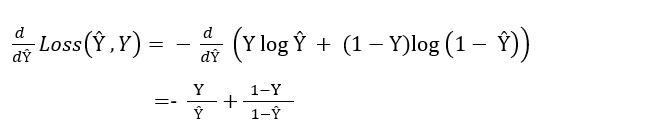
Now we can move to the second step of the backward propagation to calculate the derivation of the loss function . (Refer Fig 2).
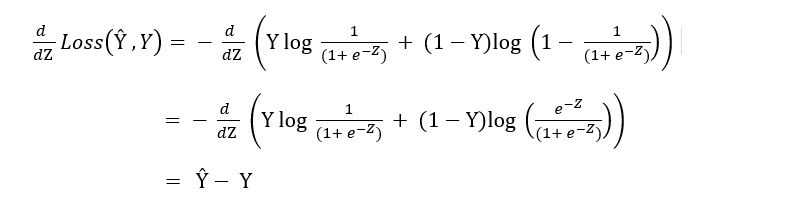
Or we can simply calculate it using chain rule of derivation.
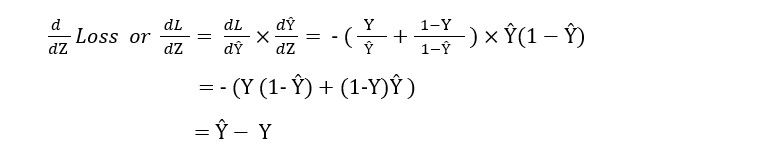
Now we move to the third step of the backward propagation to find the new values of w1, w2, and b .
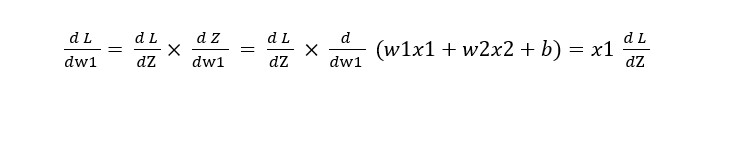
Similarly, we can calculate :
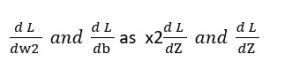
Now we can easily calculate the new value for the gradient iteration based on the understanding we had in the first post.
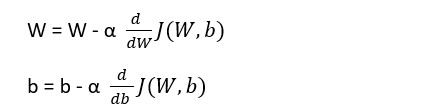
For the single training example which has two features x1 and x2, we can write new values of w’s and b for one GD iteration, as follows:
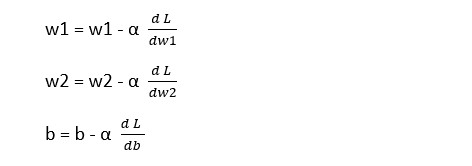
Now extend the same logic and try to calculate the same for a problem where we have m training examples and we want to know the values of w1 and w2 and b, which would be good for the entire training set.
We have 2 loops, an outer loop for m training examples and an inner loop for calculating parameters values w1,w2 and so on.

As we are calculating the average values of Loss and parameters
Loss = Loss/m
And the w and b are as..

This way we can reach out to the values of parameters for entire training set for one round of Gradient descent algorithm.

To get the understanding of Gradient Descent and Cost function from scratch, Click here.